Angles on a straight line | Geometry of straight lines

12.2 Angles on a straight line

Let us look at angles formed on one side of a straight line.

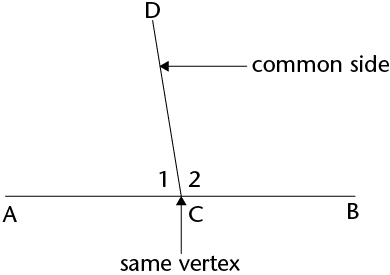
In this diagram, line segment $AB$ meets line segment $DC$ . The angle at the vertex, $C$ , where they meet, is now split into two angles: $\hat{C_1}$ and $\hat{C_2}$ .

$\hat{C_1}$ is the name for the angle at vertex $C$ labelled "1" (or $A\hat{C}D$ ).

The sum of the angles formed on a straight line

The sum of the angles that are formed on a straight line is always $180^{\circ}$ .

We can shorten this property as: $\angle$ s on a straight line.

Two angles that add up to $180^{\circ}$ are called supplementary angles.
Angles that share a vertex and a common side are said to be adjacent angles. $\hat{C_1}$ and $\hat{C_2}$ are supplementary angles.
Hence, $\hat{C_1}$ and $\hat{C_2}$ are called adjacent supplementary angles.

supplementary angles: two angles that add up to $180^{\circ}$

adjacent angles: angles that share a vertex and a common side

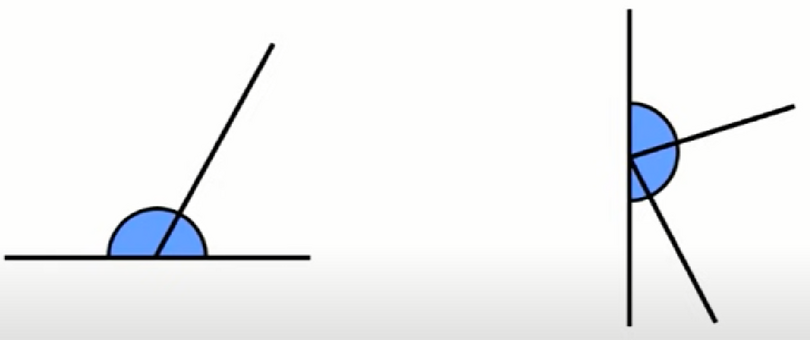
You can have more than one line meeting at the same point on a straight line. Here are a few examples of angles on a straight line.

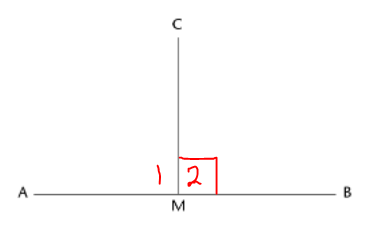
The sum of the angles on perpendicular lines

When two lines are perpendicular, the adjacent supplementary angles are both equal to $90^{\circ}$ .

In the diagram, $\hat{M_1}=\hat{M_2} =90^{\circ}$ .

A right angle is shown by forming a square at one of the right angles, like this: ⦜.

Finding unknown angles on straight lines

Worked example 12.1: Calculating unknown angles on a straight line

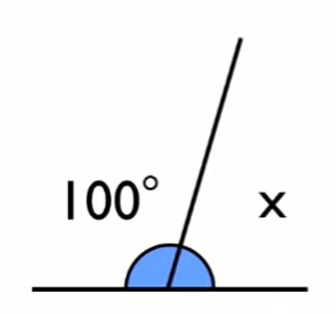
Calculate the size of $x$ .

In the diagram, we have two angles that are on the same side of the straight line. The first angle is $100^{\circ}$ and the second angle is unknown ( $x$ ). We need to calculate the size of $x$ .

We know that the two angles have a sum of $180^{\circ}$ , so we can say that:

$100^{\circ}+x=180^{\circ}$ ( $\angle$ s on a straight line)

Now we can solve this equation.

$\begin{align} x&=180^{\circ}-100^{\circ} \\ x&=80^{\circ} \end{align}$

Worked example 12.2: Calculating unknown angles on a straight line

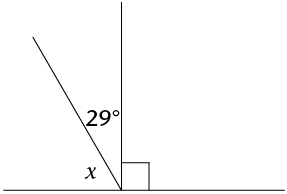
Calculate the size of $x$ .

Notice that there are three angles on the same side of the straight line. We have $x$ , an angle of $29^{\circ}$ and an angle of $90^{\circ}$ . (Remember that the ⦜ symbol on the diagram indicates a $90^{\circ}$ angle.) These three angles have a sum of $180^{\circ}$ , so we can say that:

$x+29^{\circ}+90^{\circ}=180^{\circ}$ ( $\angle$ s on a straight line)

Now we can solve this equation.

$\begin{align} x+29^{\circ}+90^{\circ}&=180^{\circ} \\ x+119^{\circ}&=180^{\circ} \\ x&=180^{\circ}-119^{\circ} \\ x&=61^{\circ} \end{align}$

There is a simpler way to solve for $x$ . It is given that we have a perpendicular line. Adjacent angles on a perpendicular line are both equal to $90^{\circ}$ . So, we have a different equation to solve.

$\begin{align} x+29^{\circ}&=90^{\circ} \\ x&=90^{\circ}-29^{\circ} \\ x&=61^{\circ} \end{align}$

Worked example 12.3: Calculating unknown angles on a straight line

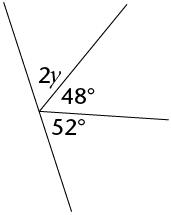
Calculate the size of $y$ .

Notice that we have three angles on the same side of the straight line. We have $2y$ , an angle of $48^{\circ}$ and an angle of $52^{\circ}$ . These three angles have a sum of $180^{\circ}$ , so we can say that:

$2y+48^{\circ}+52^{\circ}=180^{\circ}$ ( $\angle$ s on a straight line)

Now we can solve this equation.

$\begin{align} 2y+48^{\circ}+52^{\circ}&=180^{\circ} \\ 2y+100^{\circ}&=180^{\circ} \\ 2y&=180^{\circ}-100^{\circ} \\ 2y&=80^{\circ} \\ y&=40^{\circ} \end{align}$

Exercise 12.1

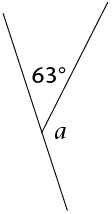
Calculate the size of $a$.

\[\begin{align} a+63^{\circ}&=180^{\circ} &(\angle\text{s on a straight line}) \\ x&=180^{\circ}-63^{\circ} \\ x&=117^{\circ} \end{align}\]

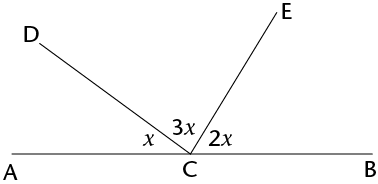
Calculate the size of:

$x$
$\hat{ECB}$

\[\begin{align} x+3x+2x&=180^{\circ} &(\angle\text{s on a straight line}) \\ 6x&=180^{\circ} \\ x&=30^{\circ} \end{align}\]
\[\begin{align} \hat{ECB}&=2x \\ &=2(30^{\circ})\\ &=60^{\circ} \end{align}\]

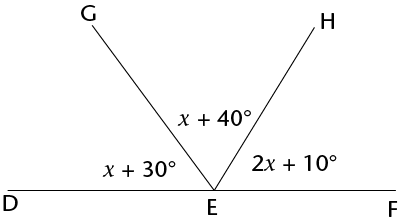
Calculate the size of:

$x$
$\hat{GEH}$

\[\begin{align} (x+30^{\circ})+(x+40^{\circ}) +(2x+10^{\circ}) &=180^{\circ} &(\angle\text{s on a straight line}) \\ 4x+80^{\circ}&=180^{\circ} \\ 4x&=100^{\circ} \\ x&=25^{\circ} \end{align}\]
\[\begin{align} \hat{GEH}&=x+40^{\circ} \\ &=25^{\circ}+40^{\circ} \\ &=65^{\circ} \end{align}\]

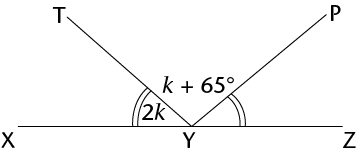
Hint: Remember that the matching curved lines “))” indicate that the angles are equal.

Calculate the size of:

$k$
$\hat{TYP}$

\[\begin{align} (2k)+(k+65^{\circ}) +(2k) &=180^{\circ} &&(\angle\text{s on a straight line}) \\ 5k+65^{\circ}&=180^{\circ} \\ 5k &=115^{\circ} \\ &=23^{\circ} \end{align}\]
\[\begin{align} \hat{TYP}&=k+65^{\circ} \\ &=23^{\circ}+65^{\circ} \\ &=88^{\circ} \end{align}\]

Introduction

Table of Contents

Vertically opposite angles

12.2 Angles on a straight line

The sum of the angles formed on a straight line

The sum of the angles on perpendicular lines

Finding unknown angles on straight lines

Worked example 12.1: Calculating unknown angles on a straight line

We know that the two angles have a sum of 180∘180^{\circ}, so we can say that:

Now we can solve this equation.

Worked example 12.2: Calculating unknown angles on a straight line

Notice that there are three angles on the same side of the straight line. We have xx, an angle of 29∘29^{\circ} and an angle of 90∘90^{\circ}. (Remember that the ⦜ symbol on the diagram indicates a 90∘90^{\circ} angle.) These three angles have a sum of 180∘180^{\circ}, so we can say that:

Now we can solve this equation.

There is a simpler way to solve for xx. It is given that we have a perpendicular line. Adjacent angles on a perpendicular line are both equal to 90∘90^{\circ}. So, we have a different equation to solve.

Worked example 12.3: Calculating unknown angles on a straight line

Notice that we have three angles on the same side of the straight line. We have 2y2y, an angle of 48∘48^{\circ} and an angle of 52∘52^{\circ}. These three angles have a sum of 180∘180^{\circ}, so we can say that:

Now we can solve this equation.

We know that the two angles have a sum of $180^{\circ}$ , so we can say that:

Notice that there are three angles on the same side of the straight line. We have $x$ , an angle of $29^{\circ}$ and an angle of $90^{\circ}$ . (Remember that the ⦜ symbol on the diagram indicates a $90^{\circ}$ angle.) These three angles have a sum of $180^{\circ}$ , so we can say that:

There is a simpler way to solve for $x$ . It is given that we have a perpendicular line. Adjacent angles on a perpendicular line are both equal to $90^{\circ}$ . So, we have a different equation to solve.

Notice that we have three angles on the same side of the straight line. We have $2y$ , an angle of $48^{\circ}$ and an angle of $52^{\circ}$ . These three angles have a sum of $180^{\circ}$ , so we can say that: